- CASE 1: You know one angle and one distance.
A,
B,
C are angles and
a
,b, and
c are distances.
So, use one of these six formulae:
| sine (A°) | = | sin (A°) | = | opposite
hypotenuse | = | a
c | | cosecant (A°) | = | csc (A°) | = | 1
sin(A°) | = | hypotenuse
opposite | = | c
a |
| cosine (A°) | = | cos (A°) | = | adjacent
hypotenuse | = | b
c | | secant (A°) | = | sec (A°) | = | 1
cos(A°) | = | hypotenuse
adjacent | = | c
b |
| tangent (A°) | = | tan (A°) | = | opposite
adjacent | = | a
b | | cotangent (A°) | = | cot (A°) | = | 1
tan(A°) | = | adjacent
opposite | = | b
a |
In this program we only use the first column above for calculations (sin, cos and tan). The second column formulae (csc, sec, and cot) are just the reciprocals of the first column values (i.e., csc(A°) = 1.0/sin(A°); sec(A°) = 1.0/cos(A°); and cot(A°) = 1.0/tan(A°) ).
CASE 2: You know two distance and NO angles.
Use these one of these three INVERSE formulae to find an angle:
A,
B,
C are angles and
a
,b, and
c are distances.
| A° | = | arcsin |  | opposite
hypotenuse | 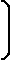 | = | arcsin |  | a
c | 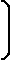 | “the set of all angles whose sin is the ratio of two sides
(the side opposite the angle and the hypotenuse)" |
| A° | = | arccos |  | adjacent
hypotenuse | 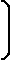 | = | arccos |  | b
c | 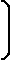 | “the set of all angles whose cos is the ratio of two sides
(the side adjacent to the angle and the hypotenuse)" |
| A° | = | arctan |  | opposite
adjacent |  | = | arctan |  | a
b |  | “the set of all angles whose tan is the ratio of two sides
(the side opposite the angle and the side adjacent to the angle)" |
In the range of angles 0° to 90° there is only one value for any arcsin, arccos, or arctan.
|