1. INTRODUCTION

Determining the reliability of knowledge based systems (KBSs) has become an important research area. This importance is due to the fact that KBSs are becoming widely used in application areas where misplaced confidence can cause large monetary losses or even loss of life. In order to legitimize the use of these systems, it is necessary to provide a foundation on which to assess KBS reliability (Nazareth and Kennedy, 1993). Therefore, developers need a set of criteria to establish reliability. Further, once such criteria are formally established researchers can evaluate existing and proposed development techniques by their ability to build KBSs that meet these criteria. For succinctness, we call these criteria reliability criteria.

In this paper, we provide a theoretical basis for judging the reliability of a KBS. Using arguments from philosophy of science, we define three main criteria by which developers can judge a KBS's reliability. Although other researchers have argued for or against specific criteria that a KBS, researchers who are grappling with the issues frequently must 'reinvent the wheel' and develop their own arguments regarding reliability criteria for a KBS. Hence, there is little agreement to the precise definitions and groupings of these criteria (Nazareth and Kennedy, 1993). This lack of agreement concerning definitions and groupings of criteria is, in part, due to the lack of theoretical foundation underpinning research regarding KBS reliability. A theoretical viewpoint provides a basis for understanding results. As such, a theory enables the generalization of results. That is, without a theory to explain results, findings may be idiosyncratic to a particular system. Worse yet, findings that might not be idiosyncratic are easier to dismiss because they lack a theoretical basis for generalizability. Finally, a theory explains why, that is, justifies a result or conclusion. For instance, redundant rules have been found to be problematic by various researchers. Despite these findings, there exists on-going debate regarding the appropriateness of redundant rules with respect to reliability concerns. Later in this paper, we argue against redundant rules because they add no new information to the KBS. Our theoretical argument explains the findings of previous researchers and enables the generalization of such findings.

To develop the reliability criteria, we conceptualize the issue of reliability, with respect to KBSs, as one of determining the criteria under which the results of KBSs should be accepted. We argue that the issue of whether to accept a KBS as reliable is similar to a major concern of philosophy of science: determining the criteria underwhich the results of scientific investigations should be accepted. Therefore, by drawing an analogy between conducting scientific investigations and constructing KBSs, we can use arguments developed for philosophy of science to establish criteria for accepting KBSs as reliable. Philosophers have debated the proper criteria by which scientific investigations should be evaluated for much longer than KBSs have existed. By utilizing the criteria developed for scientific investigations, we gain the benefit of this philosophical debate.

While we establish the reliability criteria based on the theoretical arguments from philosophy of science, some of our reliability criteria coincide with those that are based on experiences encountered while developing KBSs (such as Nguyen et al., 1985; Stachowitz and Combs, 1990, Suwa et al., 1984). Previous researchers, through trial and error, have discovered that certain characteristics enhance a KBS's reliability. Often such research has focused on a single criterion or a subset of criteria. The use of theoretical arguments provides a rigorous basis with which to establish reliability criteria. Experience-based inquiry runs into the difficulty of knowing when criteria are applicable (i.e., when are the experience-based criteria applicable to new situations?). In contrast, theoretically based criteria are generalizable.

Throughout the paper, and consistent with traditional software development (Boehm, 1981), we distinguish between issues of verification and validation. Verification is the process of showing that the resulting KBS meets its given specification (Gupta, 1991); is one building the product right (Boehm, 1981)? However, many researchers include satisfying certain structural properties in the definition of verification. In this regard, verification of KBSs has been approached from many directions. For instance, approaches based on formal methods focus on proving that the KBS satisfies its functional specification (Gamble et al., 1994, Waldinger and Stickel, 1992). Other approaches translate a developed knowledge base (KB) into a different format, which is then checked to verify the structural properties.

Validation is the process of demonstrating that the system meets the user's true requirements (Meseguer and Preece, 1995), or that the right system was built (Boehm, 1981). It is difficult to establish the validity of any software system, however establishing the validity of a KBS is often more difficult than for a conventional system (Okeefe and Oleary, 1993). With respect to KBSs, the consideration is typically if the system performs with an acceptable level of accuracy, that it reaches the correct conclusion (Zlatareva and Preece, 1993). KBSs address ambiguous problems and problems for which there is not a single correct answer, making validation particularly difficult. Others argue that the intended use of the system must be considered (Okeefe and Oleary, 1993). In other words, a system reaching the correct conclusion from a set of inputs does not mean that the system addresses the right problem. Validation must assess whether or not the system is the correct system, rather than one that provides the correct answers to what could be the wrong problem. Validation tools and techniques are less developed than verification techniques, however it is an area of increasing research emphasis and would also benefit from theoretically based criteria.

The criteria that we establish and discuss are relevant to the KB of a rule-based system, i.e., the rules. Assessing the reliability of knowledge represented using structures other than rules, e.g., objects, and of other KBS components, e.g., the inference engine, are important issues. We believe that the reliability criteria established below could be extended to other KBS representation schemes, but is beyond the scope of this paper.

2. OVERVIEW OF LAKATOS' PHILOSOPHY OF SCIENCE

To establish criteria for dependable KBSs, we use criteria from philosophy of science, specifically three criteria developed by Lakatos (Lakatos, 1970; Lakatos, 1978). In this section, we provide a brief overview of his philosophy of science, designate the relationship between elements in his arguments and the components of KBSs, and introduce Lakatos' three forms of acceptability. We discuss each form of acceptability and based on each, establish an explicit criterion for KBSs.

To place Lakatos' work in context, it is important to note that he was a contemporary of Kuhn (1970) and Popper (1968). In much of his work, Lakatos intentionally built upon the strengths of Kuhn and Popper's philosophies, while addressing the criticisms of their works. Many of these criticisms and much of the debate by these three philosophers can be found in Lakatos and Musgrave (1970). Blaug (1980:138-145) presents a thorough discussion of the relationship among their philosophies of science.

To understand Lakatos' work, we begin with brief introductions of Kuhn's and Popper's philosophies. These introduction are not intended to be summaries, we include only enough background to provide context for Lakatos' work. In relationship to Lakatos' philosophy of science, it is important to note that Popper argued that theories must be specified in a falsifiable manner and then subjected to rigorous testing to attempt to falsify the theory. Popper's focus on falsificationism was criticized as "naive falsificationism, " due to his argument that theories are separate entities that can be independently evaluated and that a single experiment can lead to acceptance or rejection of a theory. Further, such "naïve falsificationism" can lead to a decline in knowledge due to the study ever smaller areas of inquiry such that scientific content decreases (Lakatos, 1978).

Kuhn argued that science is marked by the rise and fall of paradigms, that "theories come to rise, not one at a time, but linked together in a more or less integrated network of ideas" (Blaug, 1980: 137). These paradigms, Kuhn argued, are overthrown in a revolutionary fashion whereby the burden of anomalies (unexplained results) weighs so heavily upon a paradigm that a shift occurs allowing a new paradigm to become dominant. Kuhn's work was criticized on the grounds that the term paradigm was used in an ambiguous fashion (Masterman, 1970), that his criteria for the overthrow of a theory were not scientific but sociological, and that a paradigm shift does not necessarily entail scientific progress as measured by a growth of knowledge. Further, Lakatos (1970) argued that paradigms do not shift in revolutionary fashion, but only after years of dedicated scientific work and the weight of much evidence.

In response to Kuhn and Poppers' philosophies, Lakatos argued for a "sophisticated falsificationism" as part of a methodology of scientific research programmes (MSRP). A scientific research programme (SRP) is disciplinary, in that the SRP is typically worked on by many researchers who are joined by their conviction to the SRP. Through the concept of an SRP, Lakatos incorporates the concept that theories do not exist in isolation. This addresses a weakness of naive falsificationism, which argues that theories can be assessed independently, while incorporating Kuhn's argument that groups of theories create a unified whole. According to Lakatos "we propose a maze of theories, and Nature may shout INCONSISTENT"(Lakatos, 1970:130). However, Lakatos does not argue for the overthrow of research programs. Instead, through his MSRP, he develops specific criteria for the admittance of a theory to an SRP.

3. APPLICATION OF MSRP TO KBS RELIABILITY

It is Lakatos' criteria for a theory's admittance to an SRP that make his philosophical work an appropriate foundation for examining reliability issues in KBS. His approach enables us to consider the entire rule-base of a KBS and ensure rigorous consideration of those rules, which is appropriate in the context of reliability. Finally, his dedication to the growth of knowledge ensures that the KBS criteria avoid the possibility of increasing reliability by decreasing content; i.e., we could create very reliable KBS for tiny domains, but that approach will not serve the best interests of users.

AN SRP has two major components: a hard core and a protective belt (Lakatos, 1970). The hard core forms the basis of the SRP and is considered irrefutable because it is typically too abstract and imprecise to be tested explicitly. The protective belt is comprised of theories that are derived from the hard core. The members of an SRP work to further the SRP by deriving and testing theories to form the protective belt.

Lakatos (1978) elaborates his criteria for evaluating scientific investigations by focusing on the theories offered by the SRP, referring to the acceptability of a theory. Lakatos defines three levels of acceptability. Acceptability₁ assesses the "boldness" of a theory; it must entail some "novel factual hypothesis" (Lakatos, 1978: 170). Acceptability₂ evaluates the evidence for a theory; bold theories, having met the criterion of acceptability₁, undergo severe tests to determine if they are corroborated by evidence. Acceptability₃ appraises the future performance of a theory; its reliability or "fitness to survive." Theories that meet these three criteria are deemed acceptable and are included in the protective belt of the SRP as shown in Figure 1.

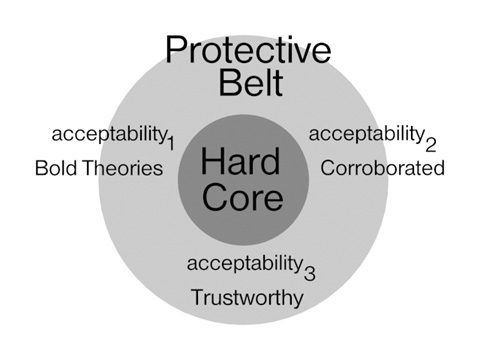
Figure 1. Hard Core, Protective Belt, and Acceptability Criteria in a Scientific Research Program

The three forms of acceptability can be applied to a KBS. To do so, we draw an analogy between a KBS and an SRP. When constructing a KBS, the system specification is analogous to the hard core of an SRP and the rules that make up the knowledge base (KB) are analogous to the theories in the protective belt. The hard core and the specification serve similar purposes, to define the problem space (domain) of interest. A typical specification for a KBS is similar to the hard core in that an original specification is also abstract, difficult to define, and must be refined. Hence, the specification is the foundation from which rules are derived and included in the KB, just as the hard core is the foundation from which theories are derived and included in the protective belt. Each rule in a KB is equivalent to one theory among the "maze of theories" that is put forth by an SRP. The analogy between a KBS and an SRP, as illustrated in Figure 2, focuses on the relationship between the rules of the KB and the theories of the protective belt. Thus, the analogy provides a theoretical justification for the KBS community's focus on rules, as opposed to the inference engine, conflict resolution strategies, or working memory to assess reliability.

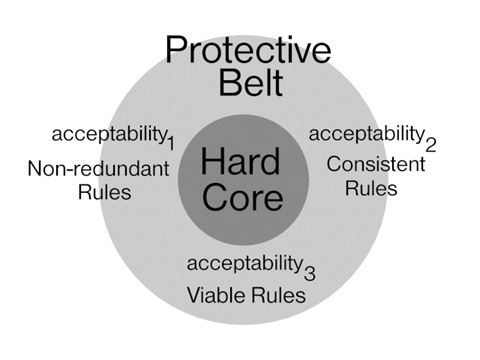
Figure 2. Specification, Knowledge Base, and Acceptability Criteria in a Knowledge-Based Systems

We extend the analogy between a KBS and an SRP to include verification and validation. Verification, in the context of KBS, is a matter of establishing that the rules faithfully represent the specification. With respect to an SRP, verification questions how thoroughly the theories cover the hard core. Validation asks if the right system was specified, questioning the quality of the specification. Therefore, validation questions the veracity of an SRP's hard core. As stated earlier, the hard core is irrefutable (Lakatos, 1970), because its veracity cannot be assessed directly. Instead, the veracity of the hard core must be considered indirectly and the forms of acceptability aid this assessment.

4. CRITERIA FOR RELIABLE KBS

Based on Lakatos' acceptability criteria and the analogy between an SRP and a KBS, we develop criteria for KBS reliability. Each form of acceptability is developed into a criterion that a KBS should possess to be deemed reliable. In addition, each criterion is comprised of more specific forms that were identified in the literature. In the discussion of each criterion, we present examples of its specific forms.

4.1 CRITERION₁: NON-REDUNDANCY

Acceptability₁ appraises the "boldness" of a theory. For a theory to meet the criterion of acceptability₁, it must have excess content over other theories. To have excess content, a theory must offer an explanation for phenomena that are not explained by the other theories encompassed within the protective belt of the SRP. There is no reason to add a theory to the protective belt of an SRP if it does not add to the body of information already encompassed by the protective belt. Lakatos points out that "one cannot decide whether a theory is bold by examining the theory in isolation" (Lakatos, 1978:171), instead a theory must be examined in the context of the other theories. Boldness is a verification issue because the theories that comprise the protective belt are questioned, not the hard core. Applying this concept to KBSs, boldness implies that each rule in a KB must explain content that is not explained by other rules, i.e., each rule must represent unique information. Therefore, the rules must be non-redundant. When focusing on reliability, there is no reason to include a rule that adds no knowledge to the KBS. To assess non-redundancy, all of the KB rules must be considered. Non-redundancy is a verification issue because non-redundancy exclusively considers the rules, not the specification.

The criterion of rule non-redundancy in a KB encompasses four forms that are identified in the literature: duplication, subsumption, unnecessary IFs and chained redundancy. Figure 3 illustrates the forms of redundancy, which are discussed following a definition of our notation.

Notation: For simplicity, our notation and subsequent examples target forward-chaining systems. Our criteria are general and apply to forward, backward, and mixed chaining systems. A rule-based system contains three major parts: the KB, the working memory, and the inference engine. The KB holds the rules that represent the specialized knowledge of the system. The working memory contains the currently available facts that may be initial premises or deduced facts. The inference engine is responsible for deducing new information by comparing the rules to the contents of working memory. If the conditions in the left-hand side (LHS) of the rule hold, then the actions in the right-hand side (RHS) of the rule are performed against working memory. Our notation in Figure 3 describes rules in which the condition/action pair is separated by "è ". If all positive literals in the condition can be matched against some existing fact in working memory, and all the negative literals in the condition are not present in working memory, then the actions are performed. We do not use remove or add commands for predicates in the RHS. Instead, we use predicates in the RHS, in which a positive literal represents an addition to working memory and a negative literal represents a deletion from working memory. Predicates in the LHS that do not appear in the RHS remain the same.

Figure 3. Forms of Redundancy

Duplication exists when two rules can succeed in the same situation and give the same results (Chang et al., 1990). This form of redundancy is illustrated by R2, which duplicates R1 (Figure 3, part a). Subsumption occurs when two rules will produce the same results, but the premises of one instance are more restrictive than the other (Chang et al., 1990). When the restrictive rule succeeds, the less restrictive instance will also succeed and a redundancy exists. We illustrate this form of redundancy by R3, which is subsumed by R1 (Figure 3, part b). Redundancy resulting from an unnecessary IF occurs when two rules are identical except for a single clause in the LHS of each rule. One rule contains the positive form of the literal and the other contains the negative form of the same literal (Nazareth, 1989). These clauses are ineffective in determining whether the rule will fire, i.e., if the other clauses of the rules are satisfied, one rule will fire with consequences identical to the second rule. This form of redundancy is illustrated by rules R4 and R5 (Figure 3, part c). Note that R4 and R5 become redundant cases of R1 when the unnecessary IFs are removed. Chained redundancy (Nazareth, 1989) exists when the consequent of a rule can be reached through a series of deductions that do not invoke the original rule. In other words, from a beginning state, a second state can be reached in two ways: directly through a single rule, or indirectly through a series of deductions. This form of redundancy is illustrated by rules R6 and R7 (Figure 3, part d), which independently deduce the same conclusion as R1.

Based on Lakatos' criterion of acceptability₁, the first criterion for a reliable KBS is that it must contain non-redundant rules. Redundancy has previously been considered undesirable due to the complications that may arise during development and maintenance (e.g., the effects associated with altering or deleting only one instance of a rule among a set of redundant rules). Despite these issues, the need to eliminate redundant rules is not a universally agreed principle. Note that Goumopoulos, Alefragis, Thranpoulidis, and Housos (1997) describe a system that requires replicated rules. Hence, there is a need to argue against redundancy from a theoretical standpoint. Redundant rules add no new knowledge to the KB, therefore redundant rules do not strengthen the KBS and should not be included. Regardless of the specific type of redundancy, the criterion of non-redundancy is not met when a rule represents information that is available via other rules, as illustrated in Figure 3. Non-redundancy can be ensured only by considering all the rules in a KBS simultaneously.

4.2 CRITERION₂: CONSISTENCY

Acceptability₂ addresses the corroboration of bold theories, i.e., those theories that meet the criterion of acceptability₁. Lakatos argues that a theory must possess "excess corroboration" over the other theories that form the protective belt. A theory is corroborated if it "entails some novel facts" (Lakatos, 1978:174). Corroboration, with respect to scientific investigations, is a matter of evaluating the empirical evidence to determine if it is consistent or inconsistent with the theory. We argue that the key ingredient relevant to KBSs is consistency.

Lakatos discusses two interpretations of acceptability₂. The first interpretation is fairly straightforward and asks if the theory has been corroborated; i.e., is it consistent with evidence? If so, the theory meets acceptability₂. This interpretation is a verification issue because it considers the protective belt, not the hard core. The second interpretation asks if the theory moves the SRP nearer to the truth; does it accurately portray the true state of nature? The second interpretation is a validation issue because it addresses the hard core of the SRP. As did Lakatos, we define two aspects of consistency: non-conflicting rules (a verification issue) and accuracy (a validation issue).

The criterion of non-conflicting rules can only be evaluated by considering the entire contents of the KB. Conflicts among rules exist when more than one rule can succeed, but with contradictory consequences, e.g., if the LHSs of two rules succeed in the same state, but the RHSs cannot both be true simultaneously. This state is undesirable in a KBS just as it is undesirable to construct a protective belt containing theories that predict contradictory states of nature to be true under identical circumstances.

The forms of conflicts encompassed by the criteria include direct, chained, and complex. Direct conflict occurs when the LHSs of two or more rules are identical, but the RHSs enter conflicting information (Figure 4, part a). Chained conflict is similar to direct conflict in that the initial LHSs are identical, but it is through a series of deductions that two conflicting states are reached (Figure 4, part b). Complex conflicts exist when two distinct LHSs can be satisfied by a particular working memory state, but produce conflicting result states. This type of conflict leads to non-determinism in the KBS, i.e., it will not always produce the same result from the same input. Because complex conflict is usually the result of not including enough details in the rules, it cannot be determined using traditional structural tests. Figure 4, part c, presents an example of complex conflict.

Figure 4. Forms of Conflict

Accuracy, the second interpretation of acceptability₂, refers to consistency with respect to validation. Accuracy concerns whether or not the system accurately reflects the problem space of the KBS. Theoretically, a KBS that does not reflect the problem space would not be considered reliable, just as an SRP that does not reflect nature would not be acceptable.

To assess accuracy, one could argue that it is necessary for the knowledge engineer to independently attempt to gather evidence to support or refute every portion of the specification. This argument ignores the process used to develop the specification, i.e., interviews with human experts, probing written documents, etc. We argue that if the knowledge encompassed by the specification was acquirable, then there is reason to believe that it reflects the domain. This line of reasoning assumes that human experts, written source documents, etc., do not intentionally deceive. However, some inaccurate knowledge may be specified, intentionally or otherwise. Hence, we advise knowledge engineers to consult multiple sources for knowledge to develop the specification. Incorporating multiple sources will expose possible inaccurate information. To paraphrase Lakatos: we propose a maze of knowledge and the analysis may shout inconsistent. When inaccuracies arise, the knowledge engineer determines the proper course of action and corrects the specification. Hence, although accuracy cannot be tested for directly because it is a validation issue, it can be addressed indirectly through the careful development of the specification.

Based on acceptability₂, the second criterion for a dependable KBS is that it must be consistent. This criterion has two perspectives: non-conflicting rules (a verification issue) and accuracy (a validation issue). Conflicting rules possess RHSs that can succeed, but that enter contradictory information. Therefore, conflicting rules can yield an inconsistent state and should not be allowed in a KB. Accuracy questions the reliability of the specification, hence it is a validation issue concerning whether or not the KB is consistent with the real-world problem domain.

4.3 CRITERION₃: VIABILITY

Acceptability₃ appraises the future performance of a theory. Lakatos refers to its trustworthiness and its fitness to survive (Lakatos, 1978). Lakatos is concerned with the future usefulness of an SRP, its ability to predict scientific phenomena. With respect to KBSs, we are concerned with the performance of the KBS, its ability to generate useful answers when used in the future; will it be a viable useful system?

When discussing trustworthiness, Lakatos' concern is the growth of scientific knowledge, which he argued could only be accomplished by considering all three forms of acceptability. In fact, Lakatos warned that appraising acceptability₃ without first assessing the other forms of acceptability could lead to accepting theories with great "total evidential support" but contain less content than earlier theories, i.e., cover less of the problem space than previous theories. This situation would lead to the degeneration of an SRP and its ultimate demise. Lakatos does not wish to achieve acceptability₃ at the expense of content.

With respect to KBSs, assessing viability without considering non-redundancy and consistency could lead to the development of KBs that contain specific rules that individually have great "total evidential support," yet do not address the breath of the problem space. Just as Lakatos is concerned that the theories comprising the protective belt adequately address the hard core of the SRP, we are concerned that the rules represent the breadth of the problem space. Consistent with Lakatos' discussion of acceptability₃, viability has two aspects: completeness and coverage. The KBS should completely address the problem space. Completeness is a verification issue because it concerns the relationship between the rules and the specification. Coverage, the second interpretation, asks if the KBS covers the true problem space. Coverage is a validation issue because its assessment extends beyond the relationship between the rules and specification to question the relationship of the specification to the underlying problem space.

Completeness implies that the rules cover the breadth of the specification. A complete KB contains the rules to move from a set of initial states to a set of goal states. If the system cannot eventually achieve a goal state from a legal initial state, then the rules are incomplete. The criterion of completeness is violated when a KB is unable to reach a goal state due to circularities or gaps in the rules. Circularity occurs when, in a chain of rules, the consequent of a rule is the antecedent of a rule fired earlier in the inference chain (Nazareth, 1989). Hence, the KBS cannot reach a goal state and would be considered incomplete, as illustrated in Figure 5, part a.

Figure 5. Forms of Incompleteness

Gaps can result from missing rules, unreachable clauses, or dead-end clauses (Nguyen et al., 1985). A rule is considered missing if there is a range of possible data values for some attribute, yet the range is not sufficiently covered by the existing rules. This form of incompleteness can cause the KBS to halt prior to reaching a goal state, as seen in Figure 5, part b. An unreachable clause is one that exists and can never be utilized by the current system as shown in Figure 5, part c. Unreachable clauses are undesirable because they serve no purpose in the KB. Further, if we reason that the knowledge engineer only includes clauses in the KB that he or she considers useful, then an unreachable clause is evidence that a rule or clause is missing. For instance, a clause or rule may be missing that changes the unreachable clause into a reachable clause (see R5 in Figure 5, part d, which corrects C1). A dead-end clause exists if it can be instantiated but does not lead to the firing of another rule (Chang et al., 1990), as shown in Figure 5, part d. Similar to an unreachable clause, dead-end clauses serve no purpose and indicate that the KBS is incomplete. The addition of a new rule to the KB or the addition of a clause to an existing rule would correct the dead-end clause.

Coverage, the second interpretation of viability, assesses an SRP's "fitness to survive," its long-term usefulness. Coverage concerns the relationship of the KBS to the real world domain, hence, it is a validation issue. The primary concern is if the KBS adequately covers the problem space? Assessing this criterion requires a clear understanding of a KBS's intended purpose. This issue is similar to the problem encountered during requirements analysis in traditional software development. Users and developers find it difficult to know the extent and breadth of uses for a software system in the early stages of development. Without a thorough understanding of the KBS's requirements, however, the knowledge engineer can only hope to build a KBS that meets the needs of the user.

Based on Lakatos' criterion of acceptability₃, the third criterion for a dependable KBS is viability. This criterion has two components: completeness (a verification issue) and coverage (a validation issue). A complete KBS addresses the breadth of problem space as defined by the specification, containing the rules to move from an initial state to a goal state. A KBS possesses coverage if it covers the breadth of the problem space.

5. CONCLUSION

Our intention is to provide a theoretical basis for reliability criteria and, based on that theory, develop definitions and criteria for reliable rule-based systems. We find that the theoretically based criteria are mainly consistent with criteria based on empirical results. As such, the empirical results provide additional support for our theoretical arguments. The addition of theoretically based criteria benefits future researchers with generalizable criteria and a context for understanding previous results.

Using Lakatos' three forms of acceptability, we developed three theoretically based criteria for a reliable rule-based systems: non-redundancy, consistency, and viability. The first criterion, non-redundancy, is solely a verification issue because it can be addressed by considering the rules of the KB exclusively. Consistency and viability both possess verification and validation components. These distinctions are consistent with acceptability₂ and acceptability₃ (Lakatos, 1978). Consistency can be partitioned into the verification and validation components of non-conflicting rules and accuracy, respectively. Viability can be similarly partitioned into completeness and coverage. Each verification criterion is described in terms of the different forms of violations that can be found in a KBS.

At this time, we address reliability criteria for rule-based systems, the most common form of KBS. Research has commenced to address verification and validation of KBSs using other forms of knowledge representation. Given that hybrid systems using both rule-based and object-oriented paradigms (Gamble and Baughman, 1996; Lee and Okeefe, 1993), case-based (Oleary, 1993), and semantic networks (Oleary, 1989) have been developed, there is a realistic need for criteria to assess the reliability of such KBSs. Future research is needed to extend the theoretical arguments presented in this paper to encompass the appropriate reliability criteria for KBSs that rely upon non-rule-based or hybrid knowledge representation schemes.

REFERENCES

Boehm, B. W. (1980) Software Engineering Economics, Prentice-Hall, Inc., Englewood Cliffs, NJ, USA.

Blaug, M. (1980) "Kuhn versus Lakatos, or paradigms versus research programmes in the history of economics," in Paradigms and Revolutions, G. Gutting (ed.), University of Notre Dame Press, Notre Dame, USA.

Chang, C.L., Combs, J.B., and Stachowitz, R.A. (1990) "A report on the expert system validation associate (EVA)," Expert Systems with Applications, Vol. 1, pp 217-230.

Gamble, R. F. and D. M. Baughman, D.M.(1996) "A methodology to incorporate formal methods into hybrids KBS verification," International Journal of Human-Computer Studies, Vol. 44, pp 213-244.

Gamble, R.F., Roman, G.C., Ball, W.E., and Cunningham, H.C. (1994) "Applying formal verification techniques to rule-based programs," International Journal of Expert Systems, Vol. 7, No. 5.

Goumopoulos, C., Alefragis, P., Thranpoulidis, K., and Housos, E. (1997) "A generic legality checker and attribute evaluator for a distributed enterprise system," 3^rd IEEE Symposium on Computers and Communications, July, pp 286-292.

Gupta, U., ed. (1991) Validating and Verifying Knowledge Based Systems, IEEE Computer Society Press, Los Alamitos, CA, USA.

Kuhn, T. (1970) The Structure of Scientific Revolutions, Second Edition, The University of Chicago Press, USA.

Lakatos, I., and Musgrave, A., eds. (1970) Criticism and the Growth of Knowledge, Cambridge University Press, Cambridge, Great Britian.

Lakatos, I. (1970) "Falsification and the methodology of scientific research programs," in Criticism and the Growth of Knowledge, I. Lakatos and A. Musgrave (eds.), Cambridge University Press, Cambridge, , pp 91-196.

Lakatos, I. (1978) Mathematics, Science, and Epistemology, Cambridge University Press, Cambridge, Great Britian.

Lee, S., and O'Keefe, R.M. (1993) "Subsumption anomalies in hybrid knowledge based systems," International Journal of Expert Systems, Vol. 6, No. 3, pp 299-320.

Masterman, M. (1970) "The nature of paradigm." In I. Lakatos and A. Musgrave, editors, Criticism and the Growth of Knowledge, Cambridge University Press, pp 59-90.

Meseguer, P. and Preece, A. D. (1995) "Verification and validation of knowledge-based systems with formal specifications," Knowledge Engineering Review, Vol. 10, No. 4, pp 331-343.

Nazareth, D.L., and Kennedy, M.H. (1993) "Knowledge based system verification and validation: The evolution of a discipline," International Journal of Expert Systems, Vol. 6, No. 2, pp 143-162.

Nazareth, D.L. (1989) "Issues in the verification of knowledge in rule-based systems," (Journal of Man-Machine Studies, Vol. 30, pp 255-271.

Nguyen, T.A. Perkins, W.A., Laffey, T.J., and Pecora, D.(1985) "Checking an expert system knowledge base for consistency and completeness," in 9^th International Joint Conference on Artificial Intelligence.

O'Keefe, R.M., and O'Leary, D.E. (1993) "Expert system verification and validation: A survey and tutorial," AI Review, Vol. 7, pp 3-42.

O'Leary, D.E. (1989) "Verification of frame and semantic network knowledge bases," in AAAI-89 Workshop on Knowledge Acquisition for KBSs.

O'Leary, D.E. (1993) "Verification and validation of case-based systems," Expert Systems with Applications, Vol. 6, pp 57-66.

Popper, K. (1968) The Logic of Scientific Discovery, Harper and Row, New York, USA.

Stachowitz, R., and Combs, J. (1990) "Completeness checking of expert systems," Technical Report A-60, Lockheed Missiles and Space Company, Inc.

Suwa, M., Scott, A.C., and Shortliffe, E.H. (1984) "Completeness and consistency in a rule-based system," in Rule-based Expert Systems, B.G. Buchanan and E.H. Shortliffe (eds.), Addison-Wesley, pp. 159-170.

Waldinger, R.J., and Stickel, M.E. (1992) "Proving properties of rule-based systems," International Journal of Software Engineering and Knowledge Engineering, Vol. 2, No. 1, pp 121-144.

Zlatareva, N., and Preece, A. (1993) "An efficient logical framework for knowledge-based systems verification," International Journal of Expert Systems, No. 7, Vol. 3.